Welcome to technical page
CLT with MATLAB |
Invariant theory <= |
Marine turbine |
Statistics |
Invariant theory
Trace, the sum of the diagonal components of the stiffness matrix of composites, is an invariant of tensorial transformation. The invariant theory was first proposed by Tsai and Melo (2014). Here, I am going to introduce the term of unequal compressive/tensile moduli into the Invariant theory. For more information, please read the published paper (link to ScienceDirect).
1, Trace
The ‘trace’ is calculated from the tensorial notation matrix,

rather than the engineering notation matrix
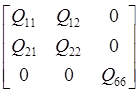
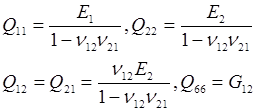
For the off-axis lamina or laminate, the tensile elastic properties can be calculated by CLT, and then the plane stress stiffness components can be extracted from the extensional stiffness matrix directly.
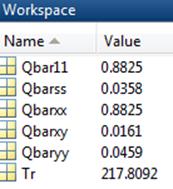
Applying the properties of IM7/977-3 (E1=191GPa, E2=9.94GPa, ν12=0.35, G12=7.79GPa), its trace can be calculated, which looks like this,
2, Tsai-Wu failure criterion
Tsai-Wu failure criterion is the one which includes compressive terms (Tsai and Wu 1971),
![]()
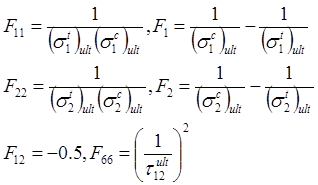
The coefficient F12 is usually determined by equibiaxial test which is nearly impossible to perform. This value is then occasionally allocated an intermediate value -0.5 (Tsai 2008).
The criterion is quadratic and is expressed in stress space. In fact, most of the current failure criteria are expressed in stress space. The Tsai-Wu failure criterion can be transformed to strain space by applying the relationship of extensional stiffness matrix,
![]()

A transformation can be applied on the strain envelope to define the rotated strain envelopes of all ply orientations,
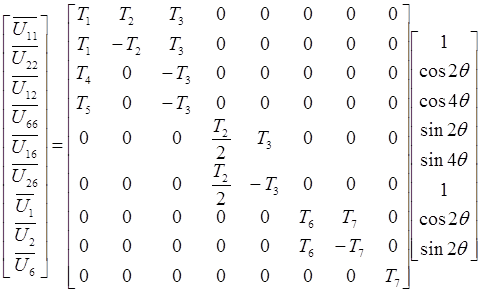
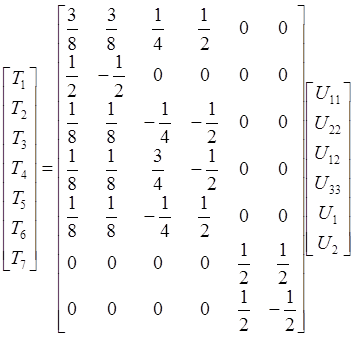
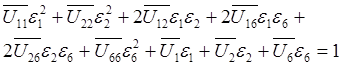
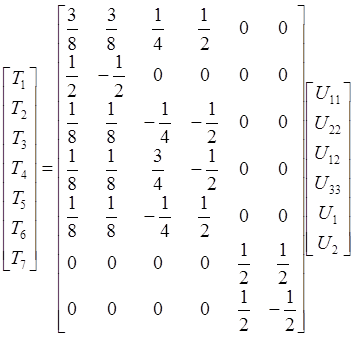

Again, for the IM7/977-3 carbon fibre-epoxy composite, the failure envelop in stress space looks like this,
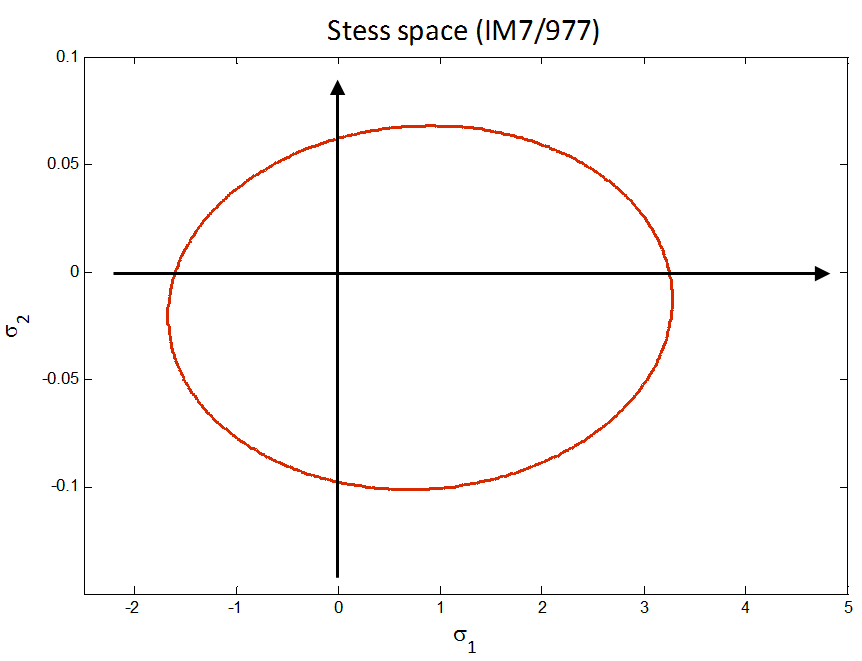
And the failure envelop in strain space looks like this,
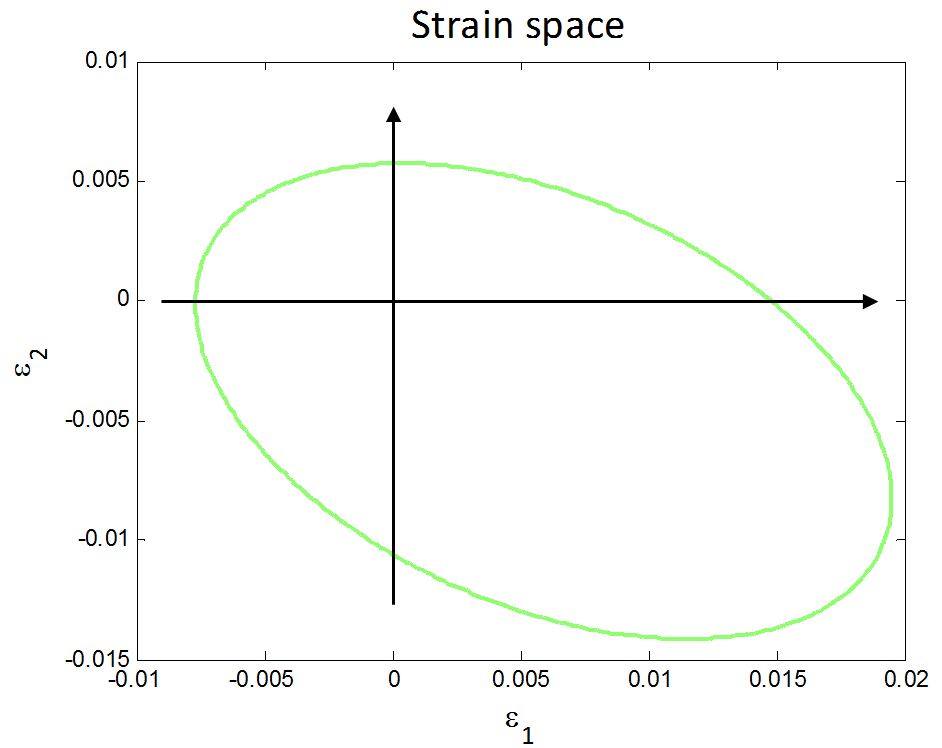
The failure envelops of different ply orientations construct a minimum shape, which was proposed as ‘omni envelop’ by (Tsai and Melo 2014). The omni envelope of T800/cytec looks like this,
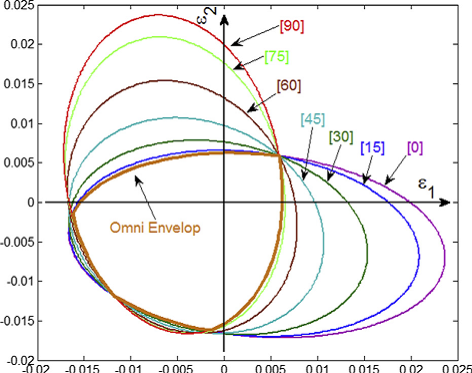
3, Unequal compressive/tensile moduli
Due to the fibre misalignment and void content which are inevitable in the manufacturing process, it is reasonable to assume that the compressive modulus is a fraction lower than the tensile modulus. So parameter is introduced to indicate the ratio of longitudinal compressive modulus to tensile modulus,
![]()
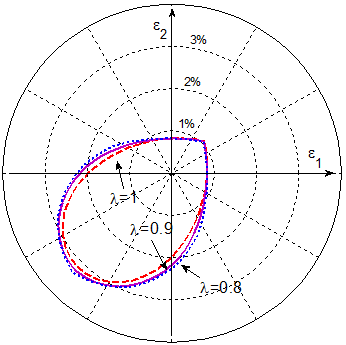
Substituting the term of unequal compressive/tensile moduli into the invariant equation, the omni envelope can be obtained. The omni envelope of T800/cytec (left) and T700/C-ply55 (right) look like this,
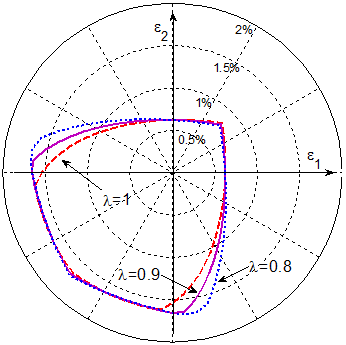
4, Implementation in MATLAB
The invariant theory can be implemented by MATLAB. To download this MATLAB code, please click here ((if you can not download it by Google Chrome, try to right click and copy the link to IE explorer)). This figure gives the GUI of the MATLAB tool.

