Software
To implement the formulae of classical laminate theory, I have developed a series of tools. Some novol formulae, which I derived for specific calculation, are also integrated in the tools, such as the equation to calculate the transverse Poisson ratio of composites. These tools are also available to process the experimental data.
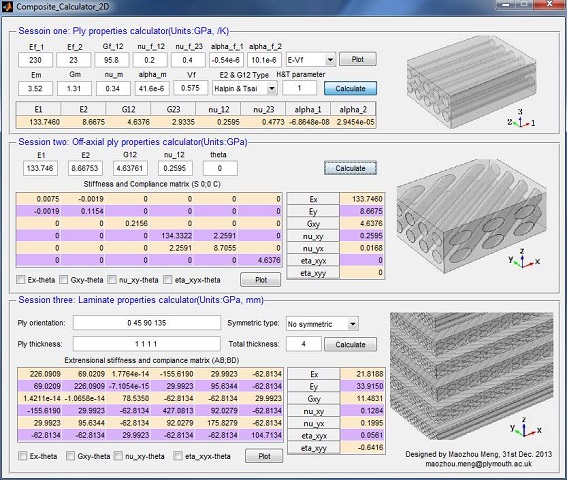
Composite calculator 2D
This software was developed to inplement CLT formulae (2D stress tensor transformation). It was complied by MATLAB 2013, 64bit. To run the software, you will need a MCR 8.1 which can be download from www.mathworks.com. The user guide including the code is also packed.
Please click here to download the Composite calculator 2D (if you can not download it by Google Chrome, try to right click and copy the address to IE explorer)
For the detailed theory of CLT, please refer to the technical pages (CLT with MATLAB)
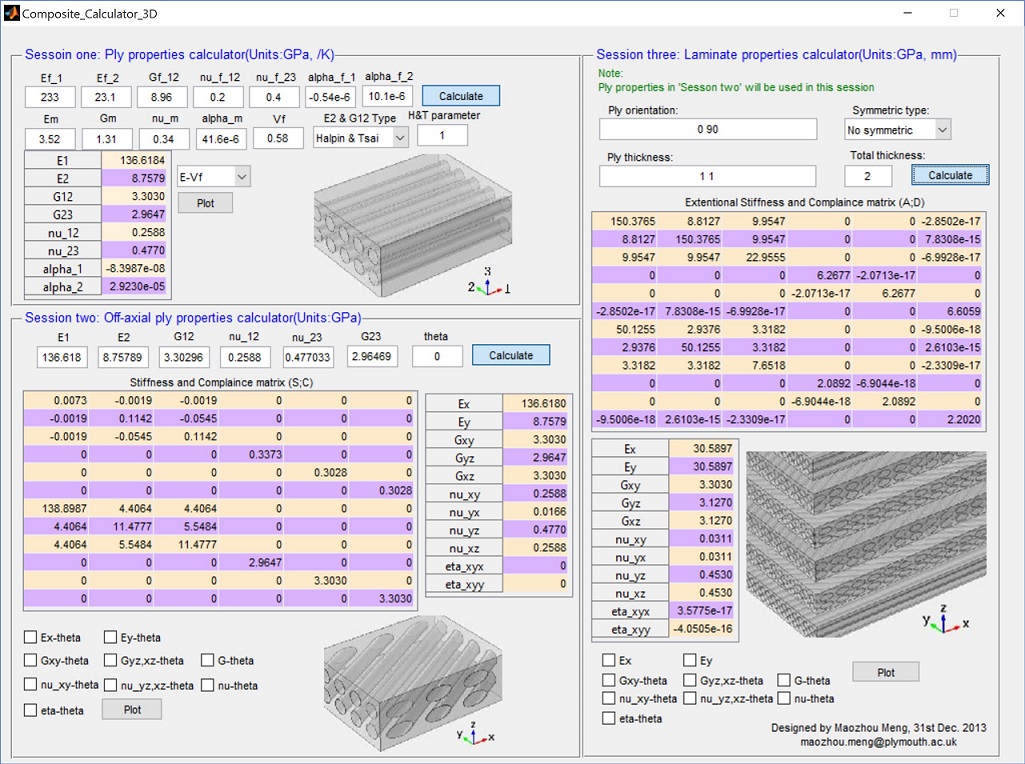
Composite calculator 3D
This software was developed to inplement CLT formulae (3D stress tensor transformation).
Please click here to download the Composite calculator 3D (if you can not download it by Google Chrome, try to right click and copy the address to IE explorer)
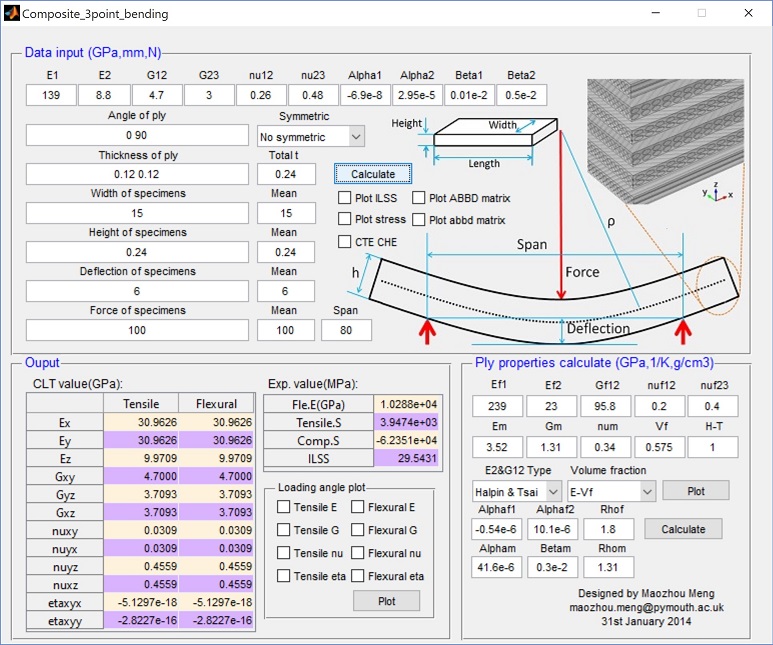
Laminated composites in bending 3-point
This software was developed to process the experimental data of laminated composites subjected to 3-point bending
Please click here to download the Laminated composites in bending 3-point (if you can not download it by Google Chrome, try to right click and copy the address to IE explorer)
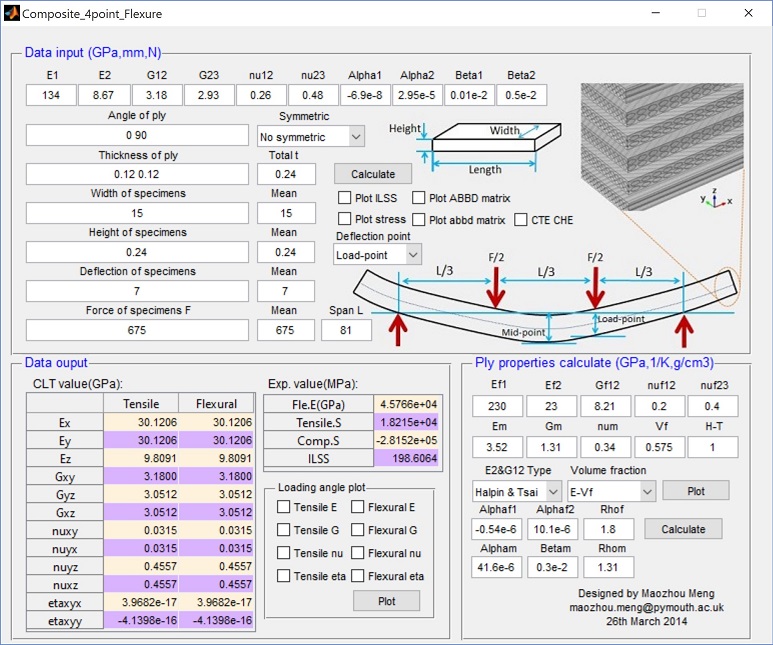
Laminated composites in bending 4-point
This software was developed to process the experimental data of laminated composites subjected to 4-point bending
Please click here to download the Laminated composites in bending 4-point (if you can not download it by Google Chrome, try to right click and copy the address to IE explorer)
Invariant theory
This software was developed to inplement the invariant theory based on the paper of (Tsai and Melo 2014)
Please click here to download the invariant theory (if you can not download it by Google Chrome, try to right click and copy the address to IE explorer)
For the detailed theory, please refer to the technical pages (invariant theory)
